My tutorials generally cover mechanical engineering topics, pretty much as they were taught when I was a student in the 1960s. For a change I decided to tackle something which did not figure on the syllabus back then. Kinematics of robot manipulators is certainly in this category and I have dedicated the study time to acquire a reasonable understanding of the subject.
Consequently, please consider these "tutorials" more as study notes broadly at the level of the early stages of an undergraduate level course. My sources are primarily video lectures and other material online. In particular I am pleased to acknowledge (and recommend) the following which have been particularly useful. However, all explanatory text and diagrams are my own composition.
Linear transformations in matrix form are the principal underlying maths in this series of tutorials. Again, this was not mainstream for mechanical engineering students fifty years ago. To get up to speed in linear algebra I highly recommend Prof. Gilbert Strang's lectures and course material on MIT's open access programme.
Linear Algebra | Mathematics | MIT OpenCourseWare
Robot basics
In these tutorials we consider a category of robots known generally as industrial robot manipulators which comprise a serial* arrangement of rigid members, known as links connected by joints which allow relative motion between pairs of links.
*another category of manipulators has links connected in parallel, a common type being the Delta robot.
There are two principal types of joint:
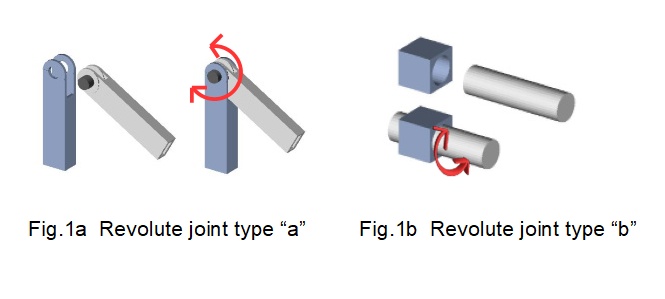
- revolute joints shown in Figs 1a and 1b below which have one rotational degree of freedom. The two types of revolute joint shown designated type a and type b are distinguished by the orientation of the axis of rotation of the joint relative to the longitudinal axis of the link.
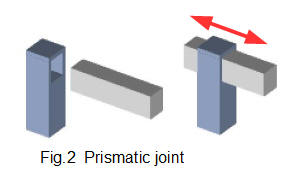
- prismatic joints shown in Fig 2, which have one linear degree of freedom.
If a manipulator has n joints each joint having one degree of freedom it is said to have a total of n degrees of freedom.
Other types of joint include spherical and universal joints which have more than one degree of freedom. These joints are often used in the gripping part of the manipulator, known as the end effector .
Robot manipulators have different combinations of links and joints. Fig. 3 below shows a manipulator where all the joints are prismatic, known as a Cartesian robot.
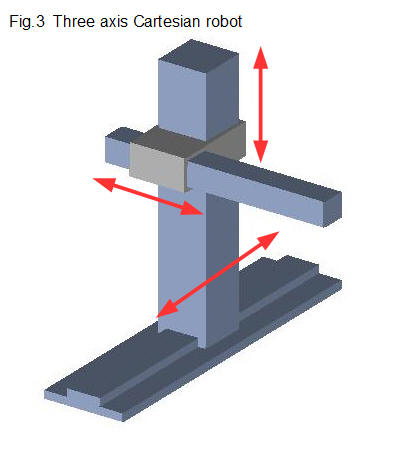
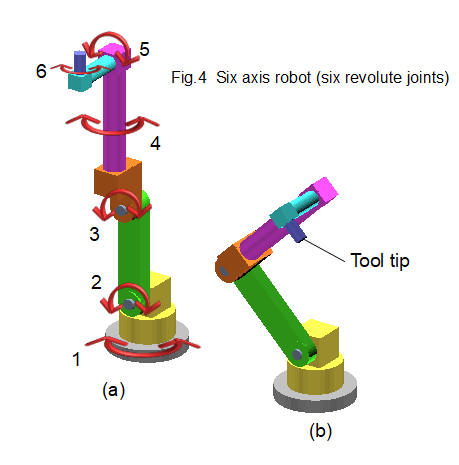
Fig. 4 below shows a robot manipulator, generally known as a six axis robot, with six revolute joints. This configuration of robot is widely used for industrial applications. The kinematic analysis in the following tutorials is based on this robot model.
The base (grey colour) represents ground. For clarity each link is illustrated in a separate colour. Joints #2 and #3 are type "a" and joints #1, #4, #5 and #6 are type "b" (as defined in Figs.1a and 1b). The actuators that rotate each joint (in most examples electrical servo or stepper motors) are not shown.
The outer extremity of the final link is called the tool tip and is the point of attachment of the end effector, for example a gripper or paint spray nozzle. The end effector itself might have additional joints but, as stated above, these are not included in our kinematic analysis.
Kinematic analysis
Kinematics is the study of the motion of a rigid body* without reference to forces acting on the body. It is concerned with determining the position (often called displacement), velocity and acceleration of a body. In these tutorials we are mainly concerned with finding the position of each robot link for a particular position of the tool tip. This position is often referred to as the tool tip pose.
*More precisely kinematics considers the motion of particles from which the motion of rigid bodies is deduced.
We can approach this task in two ways. In forward kinematics, we set the angle of each revolute joint (and the linear displacement of any prismatic joints) and then compute the position of the tool tip. In inverse kinematics we set the position of the tool tip and then compute the required angle (or displacement) of each joint. For practical applications inverse kinematics is more useful, but more complex. Forward kinematics is the subject of the next two tutorials and inverse kinematics the third.
Next: Kinematics of robot manipulators - forward kinematics 1
I welcome feedback at: