Mechanical vibrations - maths tutorial

This series of tutorials on the subject of mechanical vibrations hinges on solutions to a particular type of differential equation defined as ordinary, second order, linear, homogeneous or non-homogeneous. The purpose of this tutorial is to explain some general methods for finding these solutions. A reasonable knowledge of college level algebra and basic calculus is assumed.

Definitions of this type of differential equation are as follows.

ordinary means that all derivatives of the one dependent variable in the equation are with respect to the same independent variable (i.e. there are no partial derivatives)

second order means that the highest derivative in the equation is of the second order

linear means that the exponent of each term containing the dependent variable in the equation is one

homogeneous equations of this type equal zero; non-homgeneous equations do not

Additionally, all terms in the equations considered have constant coefficients.

In this tutorial y denotes dependent variables and x independent variables. Thus a solution means finding a function y = f(x) that satisfies the equation in question. In subsequent tutorials the dependent and independent variables are typically x (displacement) and t (time) respectively.

Solutions to homogeneous equations

We first consider a solution to the homogeneous equation which has the general form:

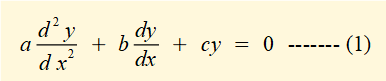
In many cases the starting point for a solution to a differential equation is to find a function that could be the basis for a solution.

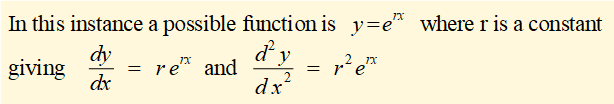
Replacing y and its derivatives in (1) above with expressions in e^rx gives:

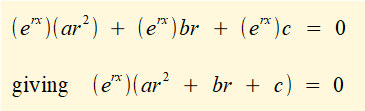
Because e^rx cannot equal zero this equation reduces to: ar² + br + c = 0 known as the characteristic equation of the original differential equation.

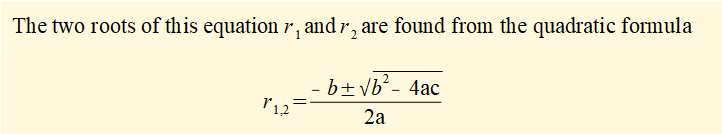
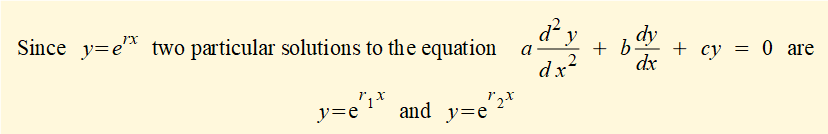
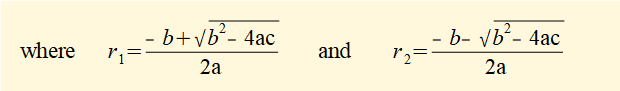
It can be shown that any linear combination of these solutions is also a solution. Hence the general solution can be expressed as:

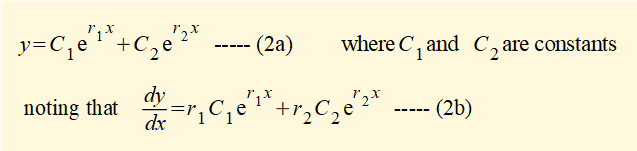
A particular solution of the original equation requires values for constants C₁ and C₂. These are found by setting initial conditions for y and dy/dx when x = 0 and substituting these values in equations (2a) and (2b) giving two equations with two unknowns (C₁ and C₂).

We now examine solutions r₁ and r₂ of the characteristic equation taking account of the value of the term (b² - 4ac) in the quadratic formula.

1. (b² - 4ac) > 0

If (b² - 4ac) > 0 then r₁ and r₂ are real numbers and the general solution can be obtained directly from equation (2) above.

2. (b² - 4ac) < 0

If (b² - 4ac) < 0 then r₁ and r₂ can be expressed as a pair of complex conjugate numbers as follows:

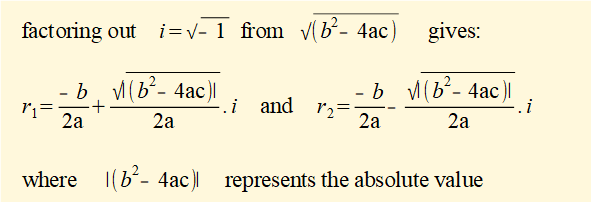
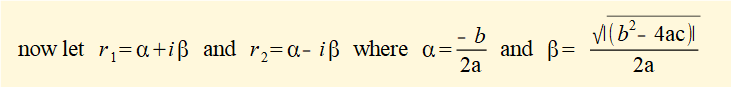
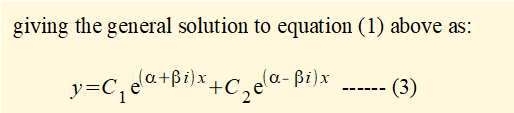
We now expand equation (3) to give:

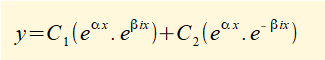
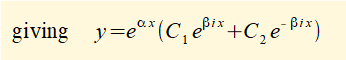
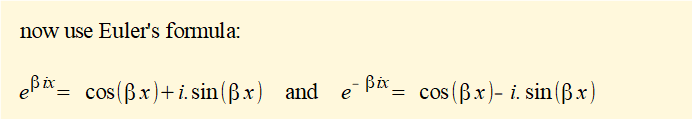
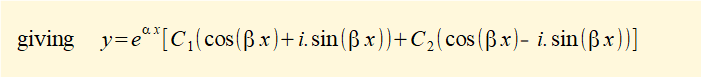
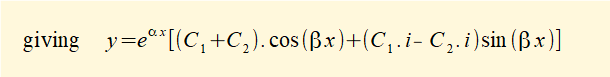
Now replace the constant terms in the above equation with "new" constants C₁ and C₂ respectively.

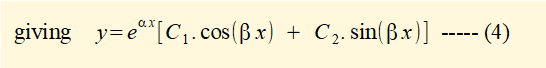
Equation(4) has no terms in i making it much easier to apply as a general solution than equation (3) above

Further simplification expresses the general solution of equation (4) as a single cosine function in the following way.

From the identity A.cos(θ) + B.sin(θ) = R.cos(θ - φ)

where R = √(A² + B²) and φ = tan^-1 (B /A)

it follows that:

y = R.e^αx cos(βx - φ) --------- (5)

where R = √(C₁² + C₂²) and φ = tan^-1 (C₂ / C₁)

3. (b² - 4ac) = 0

If (b² - 4ac) = 0 then the characteristic equation has repeated roots, r and the general solution of equation 2(a):

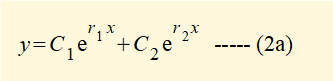
becomes y = C.e^rx ------ (2c) with constant C.

This is not a complete general solution because two initial conditions, and thus two constants, are required. However, it can be shown that equation (5) below, known as reduction of order, provides a template for solutions where there are repeated roots:

y = C₁e^rx + C₂x.e^rx -------- (5)

In subsequent tutorials we use the general solutions above to solve the homogeneous equations of motion for free vibrating systems.

Solutions to non-homogeneous equations

The general solution to this form of equation is:

the general solution for the complementary homogeneous equation

+

the particular solution for the non-homogeneous equation

This is understood better by working through an example for the following non-homogeneous equation (6):

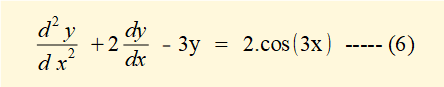
We use a cosine function f(x) = 2cos(3x) in our example because a function of this type arises in non-homogeneous equations of motion for forced vibrating systems.

Step 1 - find the general solution to the complementary homogeneous equation

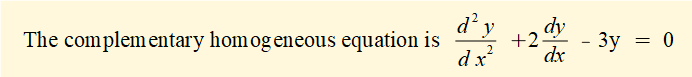
Step 2 - find the particular solution to the non-homogeneous equation

A starting point is to find two functions whose first and second derivatives replicate each other. Sine and cosine functions give a possible particular solution to equation (6) as follows:

What follows is called the method of undetermined coefficients where we find coefficients A and B by substituting y_p, y_p^/ and y_p^// in equation (6).

y_p^/ = - 3.A.sin(3x) + 3.B.cos(3x)

y_p^// = -9.A.cos(3x) - 9.B.sin(3x)

Substituting in equation (6) gives:

-9.A.cos(3x) - 9.B.sin(3x) -6.A.sin(3x) +6.B.cos(3x) -3. A.cos(3x) -3.B.sin(3x) = 2.cos(3x)

giving (- 12A + 6.B).cos(3x) + ( - 6.A - 12B).sin(3x) = 2.cos(3x)

equating coefficients for cos(3x) and sin(3x) on both sides of the equation gives:

(- 12A + 6.B) = 2 and (- 6.A - 12B) = 0

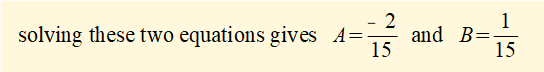
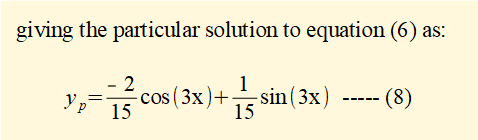
Step 3 - combine solutions

The general solution y_g to the non-homogeneous equation (6) is a combination of the solution y_c to the complementary homogeneous equation and the particular solution y_p to equation (6) which gives:

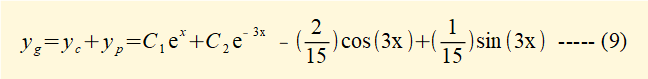
Next: Free vibrations

return to home page

I welcome feedback at:

alistair@alistairstutorials.co.uk