Four bar mechanisms - 1

Tutorials in the section mechanics of machines have so far focused on the slider and crank mechanism which has a a very important place in mechanical engineering. In fact the slider and crank is a very specific application of a more general category of mechanism known as the four bar mechanism.

In this, the first of two tutorials, we illustrate the basic configurations of a four bar mechanism. We then demonstrate two methods of analysing the displacement of the output element of the version known as the crank rocker. In the second tutorial we construct velocity and acceleration diagrams for this mechanism and consider the slider and crank mechanism, the subject of several previous tutorials, in the context of a four bar mechanism.

Basic configurations

Below we illustrate four basic configurations of a four bar mechanism. All comprise four bars (called links) connected by four revolute joints, i.e. cylindrical joints with one degree of freedom.

Movements of four bar mechanisms with revolute joints are governed by the relative lengths of the links according to what is known as Grashof's Law. In its basic form this states that continuous rotational motion of at least one link connected to a fixed link in a four bar chain is possible only if the sum of the lengths of the shortest and longest links is less than or equal to the sum of the lengths of the remaining two links. Additional criteria under Grashof's Law for specific configurations are stated below.

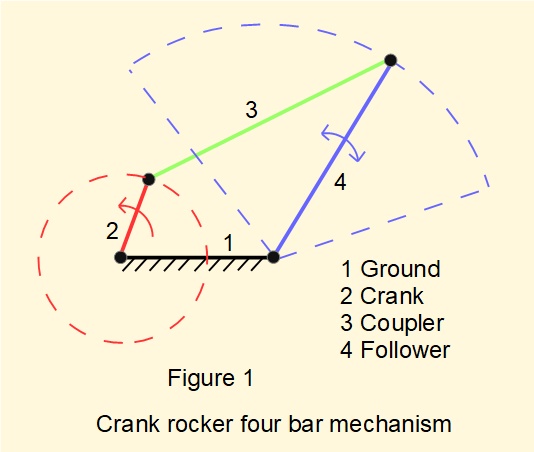
Figure 1 illustrates the crank rocker configuration where Grashof's basic criterion applies to the link lengths. The crank is capable of continuous rotation resulting in reciprocating motion of the follower, often called the rocker lever. This configuration also requires either of the two links adjacent to the shortest link to be fixed.

Figure 2 illustrates the double crank configuration where Grashof's basic criterion applies to the link lengths. Additionally, the shortest link must be fixed. Crank and follower are both capable of full rotation. This configuration is often called a drag link where the required input and output rotations are less than 360°.

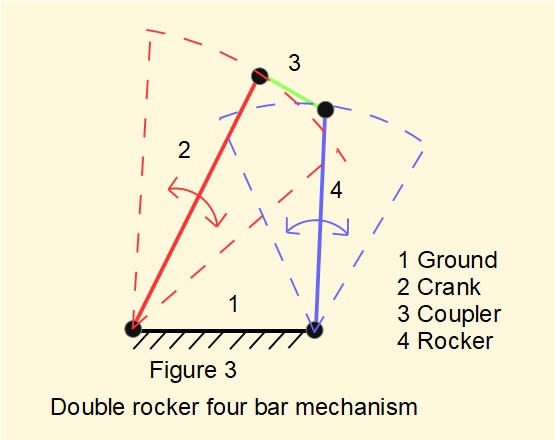
Figure 3 illustrates the double rocker configuration where the crank and rocker are restricted to reciprocating motion within defined limits. This configuration exists for two conditions: (i) where Grashof's basic criterion applies* and the coupler is the shortest link; (ii) where Grashof's basic criterion does not apply.

*note: (i) meeting Grashof's basic criterion for link lengths does not necessarily ensure that complete rotation of the input crank is possible; (ii) in this configuration complete rotation of the coupler is possible.

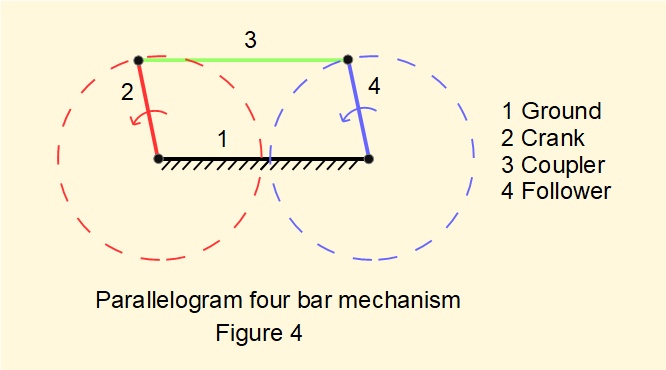
Figure 4 illustrates the parallelogram configuration. The sum of the shortest and longest links equals the sum of the remaining two links; hence from Grashof's Law continuous rotation in the form of a double crank can occur. This mechanism is very recognisable from the coupling rods that link driving wheels of railway locomotives

Kinematic analysis of a four bar mechanism

Computer software has transformed kinematic design and analysis of mechanisms for practising engineers away from traditional graphical methods and laborious calculations. However for the student it is instructive to consider displacement of the follower element using first principles. We will do this for the crank rocker configuration of a four bar mechanism.

Figure 5 above shows a crank rocker four bar mechanism where L₁ is the fixed link, L₂ the crank input, L₃ the coupler and L₄ the rocker lever output. If we define the position of the input crank as angle θ₁₂ the position of the rocker is determined by angles θ₁₃ and θ₁₄. Our task is to find expressions for unknown angles θ₁₃ and θ₁₄ in terms of known angle θ₁₂ and known link lengths L₁, L₂, L₃ and L₄. We can can then express point C or any other point on rocker L₄ in terms of x and y co-ordinates. This process is called position analysis.

We consider two approaches to position analysis:

• Derivation using geometry


• Derivation using vector loop equations

Derivation of position using geometry

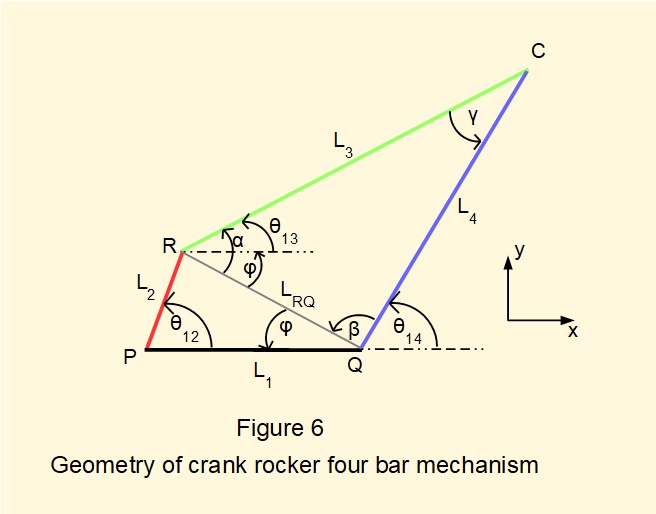
Figure 6 shows the mechanism of Figure 5 with positions of joints designated P, R, C, Q and additional line L_RQ. Angles α, β, γ, and φ are defined as shown. The strategy is to develop expressions progressively for all angles using the cosine and sine laws.

Firstly find an expression for angle φ containing known parameters.

By law of cosines for triangle RPQ:

L_RQ² = L₁² + L₂² - 2.L₁.L₂.cosθ₁₂

gives:   L_RQ = √[L₁² + L₂² - 2.L₁.L₂.cosθ₁₂]

By law of sines:

sinφ/L₂ = sinθ₁₂/L_RQ

gives:   φ = sin^-1[L₂.sinθ₁₂/L_RQ]

Now find an expression for angle α containing known parameters.

By law of cosines for triangle CRQ:

L₄² = L_RQ² + L₃² - 2.L_RQ.L₃.cosα

gives   cosα = [L_RQ² + L₃² - L₄²]/2.L_RQ.L₃

gives   α = cos^-1[{L_RQ² + L₃² - L₄²}/2.L_RQ.L₃]

Now find an expression for angle β containing known parameters.

By law of sines:

sinβ/L₃ = sinα/L₄

gives:   β = sin^-1[L₃.sinα/L₄]

From Figure 6:

θ₁₃ = α - φ

θ₁₄ = π - [β + φ]

γ = π - [α + β]

We now have sufficient parameters to determine positions of the rocker and coupler in terms of angles θ₁₃ and θ₁₄ with respect to crank angle θ_12.

And finally, designating the origin for co-ordinates at joint R, co-ordinates x_c and y_c of point C are given by:

x_c = L₁ + L₄.cosθ₁₄

y_c = L₄.sinθ₁₄

Alternative configuration of the mechanism

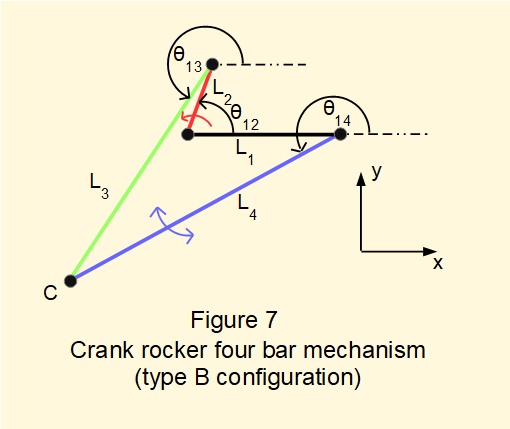
Note that the configuration of the crank rocker mechanism with link dimensions shown in Figures 5 and 6 is not unique. Consider the configuration with links of identical dimensions shown in Figure 7 below for the same crank angle θ₁₂. In this case the coupler/rocker joint C lies below the horizontal axis of the fixed link. The expressions for position analysis developed above are equally valid for both configurations.

We will call the configuration shown in Figures 5 and 6 type A and the configuration shown in Figure 7 type B.

*Types A and B are sometimes called respectively "open" and "cross" configurations.

Computing and plotting position of the rocker

L₁ = 2,   L₂ = 1,   L₃ = 3.5,   L₄ = 4

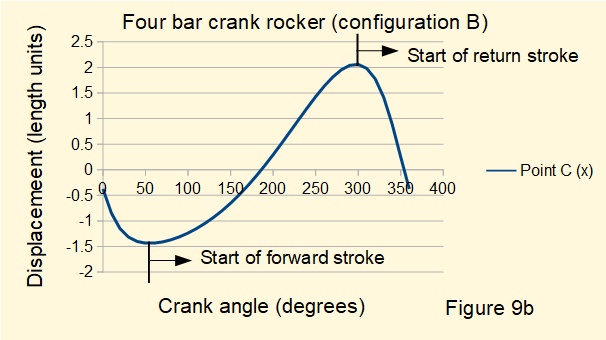
Figures 9a and 9b below show displacement of point C on the X co-ordinate for one complete revolution of the crank rotating in a counter-clockwise direction respectively for configurations A and B.

It is clearly seen that configuration A provides a fast forward and slow return stroke of the rocker. Configuration B has the opposite characteristic. It is also seen that these characteristics reverse if the crank rotates in the opposite direction. Note the similarity with complementary configurations of offset slider and crank mechanisms outlined in a previous tutorial.

The animation below illustrates the motion of both configurations with counter-clockwise rotation of the crank.

Derivation of position using vector loop equations

The geometrical analysis provided an algorithm allowing us to compute angles θ₁₃ and θ₁₄ for given crank angles θ₁₂ but does not provide equations directly expressing angles θ₁₃ and θ₁₄ in terms of known angle θ₁₂. This can be done using the method of vector loop equations.

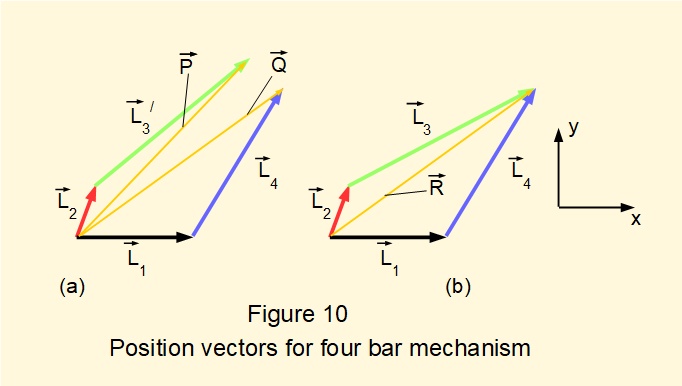
When a series of links is joined to form a mechanism where the motion is constrained, the position vectors* of the links form a vector loop. The concept is illustrated in Figure 10 above. In view (a) bars #3 and #4 are not linked and the arrangement is not constrained. Vector P = L₂ + L₃^/ and vector Q = L₁ + L₄. Clearly P ≠ Q .

*In this context the origin of each position vector is the preceding joint, not a common origin.

In view (b) links #3 and #4 are joined and the arrangement is constrained. Vector R = L₂ + L₃ = L₁ + L₄. The resulting vector loop equation is defined as:

L₂ + L₃ = L₁ + L₄

The vector loop equation is often stated in the form:

L₂ + L₃ - L₁ - L₄ = 0

We now develop the vector loop equation for the four bar mechanism. Refer to Figure 11 above showing unit vectors i and j.

The vector loop equation is:

L₂ + L₃ = L₁ + L₄ where:

L₁ = L₁cos(0°).i + L₁sin(0°).j = L₁.i + 0.j

L₂ = L₂cos(θ₁₂).i + L₂sin(θ₁₂).j

L₃ = L₃cos(θ₁₃).i + L₃sin(θ₁₃).j

L₄ = L₄cos(θ₁₄).i + L₄sin(θ₁₄).j

Taking i and j components separately in the loop equation above gives:

[L₂cos(θ₁₂) + L₃cos(θ₁₃)].i = [L₁ + L₄cos(θ₁₄)].i

[L₂sin(θ₁₂) + L₃sin(θ₁₃)].j = [0 + L₄sin(θ₁₄)].j

giving scalar equations:

[L₂cos(θ₁₂) + L₃cos(θ₁₃)] = [L₁ + L₄cos(θ₁₄)] ......... (1)

[L₂sin(θ₁₂) + L₃sin(θ₁₃)] = [0 + L₄sin(θ₁₄)] .......... (2)

Designating crank angle θ₁₂ a known angle, we need to solve for two unknowns, θ₁₃ and θ₁₄. We choose to solve for θ₁₄ first and will eliminate θ₁₃ from equations (1) and (2).

Rearrange equations (1) and (2) as follows:

L₃cos(θ₁₃) = [-L₂cos(θ₁₂) + L₄cos(θ₁₄) + L₁ ] ......... (3)

L₃sin(θ₁₃) = [-L₂sin(θ₁₂) + L₄sin(θ₁₄)] .......... (4)

Now square both sides of equations (3) and (4) giving:

L₃²cos²(θ₁₃) = [-L₂cos(θ₁₂) + L₄cos(θ₁₄) + L₁ ]² ......... (5)

L₃²sin²(θ₁₃) = [-L₂sin(θ₁₂) + L₄sin(θ₁₄)]² .......... (6)

Adding equations (5) and (6) gives:

L₃²[cos²(θ₁₃) + sin²(θ₁₃)] = [-L₂cos(θ₁₂) + L₄cos(θ₁₄) + L₁]² + [-L₂sin(θ₁₂) + L₄sin(θ₁₄)]² ......... (7)

as    [cos²(θ₁₃) + sin²(θ₁₃)] = 1  equation (7) becomes:

L₃² = [-L₂cos(θ₁₂) + L₄cos(θ₁₄) + L₁]² + [-L₂sin(θ₁₂) + L₄sin(θ₁₄)]² ......... (8)

Expanding the RHS of equation (8) gives:

\(\normalsize {L_3}^2 = ( L_2. cos\theta_{12})^2 + (L_4.cos\theta_{14})^2 + L_1^2 - (2.L_2.cos\theta_{12})(L_4.cos\theta_{14}) - 2.(L_1.L_2.cos\theta_{12})+ 2.(L_1.L_4.cos\theta_{14}) + (L_2.sin\theta_{12})^2 + (L_4.sin\theta_{14})^2 - 2.(L_2.sin\theta_{12}.L_4.sin\theta_{14}) \: ......... (9) \)

Noting that:   \(\normalsize ( L_2. cos\theta_{12})^2 + (L_2.sin\theta_{12})^2 = {L_2}^2 \newline and \: \: (L_4.cos\theta_{14})^2 + (L_4.sin\theta_{14})^2 = {L_4}^2 \)    rearranging terms in equation (9) gives:

\(\normalsize {L_1}^2 + {L_4}^2 + {L_2}^2 - {L_3}^2 - 2.{L_1}.{L_2}.cos\theta_{12} + 2.{L_1}.{L_4}.cos\theta_{14} - 2.{L_2}.{L_4}(sin\theta_{12}.sin\theta_{14} + cos\theta_{12}.cos\theta_{14}) = 0 \:......... (10) \)

Rearranging terms in equation (10) and dividing both sides by (2.L₂.L₄) gives:

\(\Large \frac {{L_1}^2 + {L_4}^2 + {L_2}^2 - {L_3}^2}{2.L_2.L_4} - \frac {{L_1}.cos\theta_{12}}{{L_4}} + \frac{{L_1}.cos\theta_{14}}{{L_2}} \)

\(\normalsize = (sin\theta_{12}.sin\theta_{14} + cos\theta_{12}.cos\theta_{14}) \:......... (11) \)

In equation (11) define the following constant terms:

\(\normalsize K_1 = \Large \frac {L_1}{L_2} \: \: \: \normalsize K_2 = \Large \frac {L_1}{L_4} \: \: \: \normalsize K_3 = \Large \frac {{L_1}^2 + {L_4}^2 + {L_2}^2 - {L_3}^2}{2.L_2.L_4} \)

and use the identity:    \(\normalsize (sin\theta_{12}.sin\theta_{14} + cos\theta_{12}.cos\theta_{14}) = cos(\theta_{12} - \theta_{14}) \)    to give:

\(\normalsize \pmb {K_1.cos\theta_{14} - K_2.cos\theta_{12} + K_3 = cos(\theta_{12} - \theta_{14})} \:.........(12) \)

Equation (12) is called Freudenstein's equation

(Note we can derive a similar form of this equation containing cosθ₁₂ and cosθ₁₃ by eliminating θ₁₄ from equations (1) and (2) above.)

Now we must solve Freudenstein's equation for θ₁₄. One method is as follows.

Substitute the following "half angle" identities into equation (12).

\(\normalsize sin\theta_{14} = \normalsize \cfrac {2.tan (\cfrac {\theta_{14}}{2})}{1 + tan^2(\cfrac{\theta_{14}}{2})} \: \: \: \: \: \: \: \normalsize cos\theta_{14} = \normalsize \cfrac {1 - tan^2(\cfrac{\theta_{14}}{2})}{1 + tan^2(\cfrac{\theta_{14}}{2})} \)

then use the reverse identity    \(\normalsize cos(\theta_{12} - \theta_{14}) = (sin\theta_{12}.sin\theta_{14} + cos\theta_{12}.cos\theta_{14}) \)

and let   \(\normalsize tan (\cfrac {\theta_{14}}{2}) = P \)    to give:

\(\normalsize \cfrac {K_1 - K_1.P^2 -2.P.sin\theta_{12} - cos\theta_{12}.(1 - P^2)}{(1 +P^2)} - K_2.cos\theta_{12} + K_3 = 0 \)

multiply both sides by  (1 + P²)   to give:

\(\normalsize K_1 - K_1.P^2 - 2.P.sin\theta_{12} - cos\theta_{12} + cos\theta_{12}.P^2 - K_2.cos\theta_{12} - K_2.cos\theta_{12}.P^2 +K_3 + K_3.P^2 = 0 \)

and express this equation as a quadratic in P giving:

\(\normalsize [cos\theta_{12} - K_1 - K_2.cos\theta_{12} + K_3].P^2 - [2.sin\theta_{12}].P + [K_1 - (K_2 + 1).cos\theta_{12} + K_3] \newline = 0 \:..........(13) \)

Now solve equation (13) for P using the quadratic formula for   aP² + bP + c = 0   where:

\(\normalsize a = cos\theta_{12} - K_1 - K_2.cos\theta_{12} + K_3\)

\(\ b = -2.sin\theta_{12} \)

\(\ c = K_1 - K_2.cos\theta_{12} - cos\theta_{12} + k_3 \)

Giving two solutions    \(\ P = tan (\cfrac {\theta_{14}}{2}) = \cfrac {-b \pm \sqrt(b^2 -4ac)}{2a} \:.........(14) \)

from which    \(\ \theta_{14} = 2.tan^{-1} (\cfrac {\theta_{14}}{2}) \)

Figure 12 below plots the X co-ordinate of point C against crank angle θ₁₂ for the four bar mechanism illustrated in Figure 8 and computed using the solution:

\(\ tan (\cfrac {\theta_{14}}{2}) = \cfrac {-b \pmb{+} \sqrt(b^2 -4ac)}{2a} \)

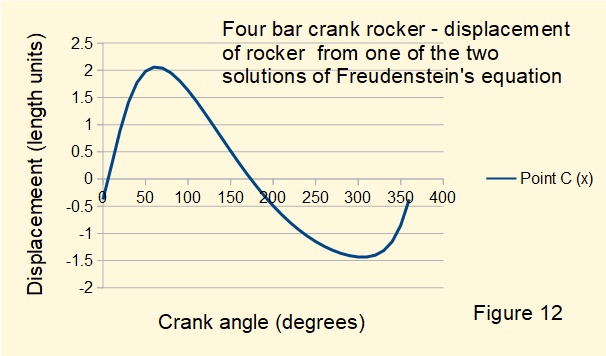
The plot replicates Figure 9a for the type A configuration with slow return characteristic derived from geometrical analysis. Correspondingly, plotting the X co-ordinate of point C against crank angle θ₁₂ using the alternative solution:

\(\ tan (\cfrac {\theta_{14}}{2}) = \cfrac {-b \pmb{-} \sqrt(b^2 -4ac)}{2a} \)

replicates the displacement of the type B configuration with quick return characteristic.

In the next tutorial we construct velocity and acceleration diagrams for this four bar mechanism and consider the slider and crank mechanism from previous tutorials in the context of a four bar mechanism.

Next:  Four bar mechanisms - 2

I welcome feedback at:

alistair@alistairstutorials.co.uk