Four bar mechanisms - 2

In this, the second of two tutorials on the subject of four bar mechanisms, we construct velocity and acceleration diagrams for the crank rocker mechanism considered in the previous tutorial and examine the slider crank mechanism in the context of a four bar mechanism.

Principles of velocity and acceleration diagrams

Velocity and acceleration diagrams are drawn to scale beginning with known values. Unknown values are then measured directly from the completed diagrams. It is also possible to obtain unknown values from the geometry of the diagrams.

A key point when constructing velocity and acceleration diagrams is the distinction between absolute and relative quantities. Consider the velocity diagrams in Figure 1 below which represent velocities of two pin joints in a mechanism designated a and b. Arrows v_a and v_b represent direction and magnitude of the absolute velocities of points a and b respectively relative to point o which indicates a "ground point" in a common frame of reference.

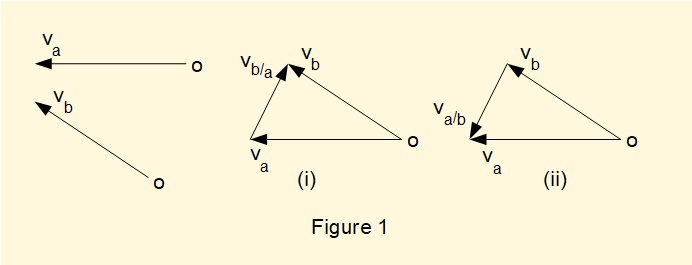
To create the velocity diagrams, v_a and v_b are connected at their common reference point o and the diagram closed by a third arrow. In (i) the arrow direction represents the relative velocity v_b/a meaning the velocity of point b relative to point a. In (ii) the arrow v_a/b represents the velocity of point a relative to point b.

Acceleration diagrams are constructed in a similar way to velocity diagrams bearing in mind that directions of velocity and acceleration for a point are not necessarily the same. Acceleration diagrams must also take into account that rotational motion of any point always has a radial component of acceleration directed towards the centre of rotation and a tangential component of acceleration when the point is subject to angular acceleration. The diagram below shows an acceleration diagram for the crank pin A of a rotating crank arm.

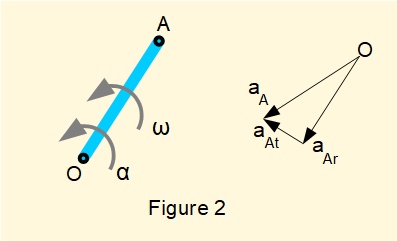
In this diagram point A rotates about point O with angular velocity ω and angular acceleration α. The diagram represents a snapshot for a specific crank angle.

• a_Ar is the radial (centripetal) acceleration of point A relative to point O with direction from A towards O resulting from angular velocity ω.


• a_At is the tangential acceleration of point A relative to point O resulting from angular acceleration α.


• a_A is the resultant acceleration of point A relative to point O.

Be aware that point O has two slightly different interpretations in the above depending on context. In one respect point O is the centre of rotation of the crank arm AO. In a more general context it represents a ground frame of reference.

Note that arrows representing velocity and acceleration in the above diagrams are not necessarily connected as vectors in the sense that conventional representation of vector addition and subtraction does not always apply. For this reason quantities are not denoted in conventional vector form. This point is explained diagrammatically in a previous tutorial.

Velocity diagram for four bar crank rocker mechanism

Figure 3 below shows the configuration of the four bar mechanism we used in the previous tutorial illustrated with crank angle θ₁₂ = 120°. Note the four revolute joints are designated A, B, C and D.

Link lengths are (using metres as a unit of length for convenience):

L₁ = 2 m,   L₂ = 1 m,   L₃ = 3.5 m,   L₄ = 4 m

The angular velocity of crank arm L₂ is designated ω_AB. For this example ω_AB = 2π radians/s.

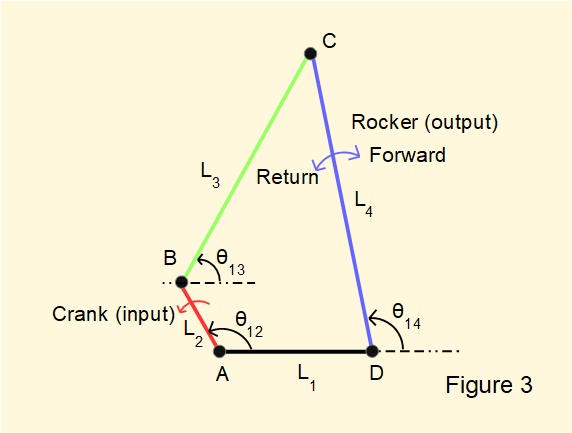
We now construct a velocity diagram for the crank mechanism for this crank angle.

The diagram has the following components:

• velocity of point B relative to point A (ground) designated v_B/A


• velocity of point C relative to point B designated v_C/B


• velocity of point C relative to point D (ground) designated v_C/D which is also the velocity of point C relative to point A as point A is also a ground point. Thus we refer to this velocity as v_C/A

We know the following:

• The line of action of v_B/A is perpendicular to the crank arm L₂. Its magnitude is
  ω_AB.L₂ = (2π).(1) = 2π. The crank arm rotates in a counter-clockwise direction which determines the direction of v_B/A


• Assuming the coupler is rigid the motion of point C relative to point B must be purely rotational. Thus the line of action of v_C/B is perpendicular to BC. Its magnitude is ω_BC.L₃.


• The line of action of v_C/A is perpendicular to the follower. Its magnitude is ω_CD.L₄

Note at this stage ω_BC and ω_CD are unknown.

Figure 4 below shows the lines of action of these velocities.

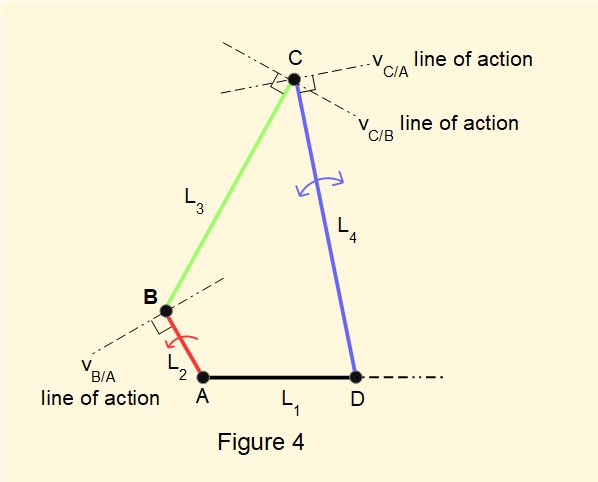
We now construct the velocity diagram. Firstly, calculate the magnitude of v_B/A and draw the arrow to scale along the line of action. The head of the arrow represents point B relative to ground point A at the tail. Now draw the line of action of v_C/B through point B and the line of action of v_C/A through point A. The point of intersection of these two lines represents point C and determines the magnitude and direction of v_C/B and v_C/A.

Figure 5 below illustrates this construction.

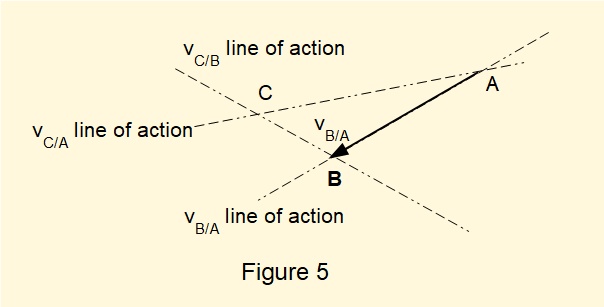
The completed velocity diagram is shown below. Note that magnitude and direction of v_C/B and v_C/A are both determined by this construction, the head of the arrow representing the velocity at that point relative to the point at the tail.

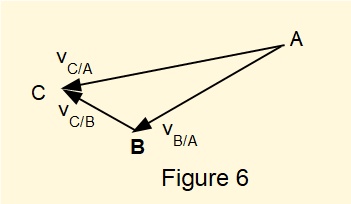
Values scaled from well drawn velocity diagrams are sufficiently accurate for practical purposes. Alternatively, velocities can be calculated directly from the diagram.

Referring to Figure 3, angles computed from the algorithm for position analysis for crank angle
θ₁₂ = 120° (see the previous tutorial) are:

θ₁₃ = 60.8°

θ₁₄ = 101.4°

From geometry, angles in triangle ABC in Figure 6 are resolved as follows:

angle A = 18.6°

angle B = 120.8°

angle C = 40.6°

Given the magnitude of velocity vector v_B/A = 2π it follows from the law of sines that:

\(\normalsize \cfrac{BC}{sinA}=\cfrac{AC}{sinB}=\cfrac{AB}{sinC} \)  to give   \( \cfrac{AB}{sinC}=\cfrac{2.\pi}{sin40.6\degree}=9.65 \)

Giving BC = magnitude of v_C/B = 3.01 m/s   and   AC = magnitude of v_C/A = 8.29 m/s

The magnitude of the corresponding angular velocities for the coupler (ω₁₃) and rocker (ω₁₄) are thus:

ω₁₃ = v_C/B/3.5 = 0.86 radians/s

ω₁₄ = v_C/A/4.0 = 2.07 radians/s

Velocity plots

Figure 7 below plots velocity v_C/A at end point C of the rocker for a complete crank cycle derived from velocity diagrams constructed at intervals of 10 degrees.

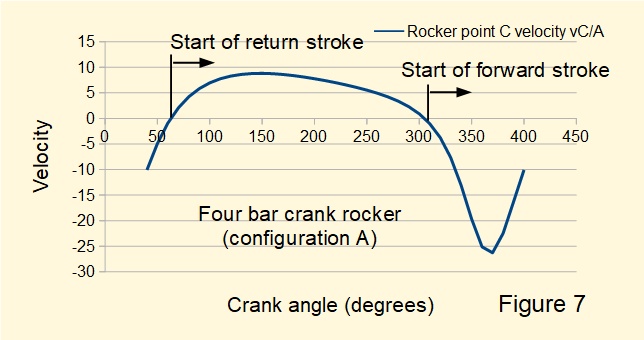
The diagram clearly shows the fast forward/slow return characteristic of this configuration. Figure 8 below shows the corresponding plot for angular velocity of the rocker ω₁₄. Note the convention of positive counter-clockwise rotation (return stroke) and negative clockwise rotation (forward stroke) replicated in the velocity plot.

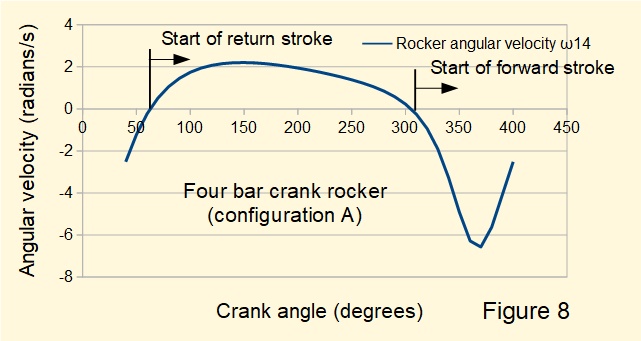
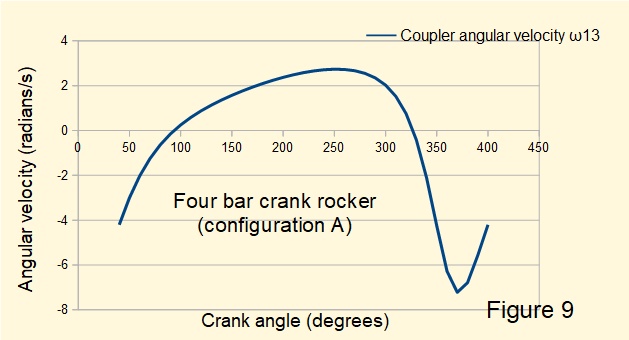
Figure 9 below plots the angular velocity of the coupler ω₁₃ over one crank cycle. Note that changes of direction of rotation of the coupler do not occur at transitions between forward and return strokes of the rocker.

Derivation of angular velocity by differentiation

There is a very elegant method for determining angular velocities ω₁₃ and ω₁₄ by differentiating the vector loop equation for position analysis from the previous tutorial expressed in exponential complex form, namely:

\(\large\ L_2 + L_3 = L_1 + L_4 \) expressed as:

\(\large\ {L_2}.e^{i. \theta _{12}} + {L_3}.e^{i. \theta _{13}} = L_1 + {L_4}.e^{i. \theta _{14}} \)

differentiating θ₁₂, θ_{13 and θ14 with respect to time gives:}

\(\large\ i.{L_2} .\omega_{12}.e^{i. \theta _{12}} + i.{L_3}.\omega_{13}.e^{i. \theta _{13}} = i.L_4.\omega_{14}.e^{i. \theta _{14}} \)

Eliminating i and rearranging gives:

\(\large\ {L_3}.\omega_{13}.e^{i. \theta _{13}} - L_4.\omega_{14}.e^{i. \theta _{14}} = -{L_2} .\omega_{12}.e^{i. \theta _{12}} ......... (1) \)

To solve for θ₁₃ in terms of θ₁₂ multiply equation (1) by e^-i.θ₁₄ giving:

\(\large\ {L_3}.\omega_{13}.e^{i. (\theta _{13}-\theta_{14})} - L_4.\omega_{14} = -{L_2} .\omega_{12}.e^{i. (\theta _{12}-\theta_{14})} \)

Applying Euler's formula:   \(\large\ e^{i\theta} = cos \theta +i.sin \theta \)   gives:

\(\large\ L_3.\omega_{13}[cos(\theta_{13}-\theta_{14}) + i.sin(\theta_{13}-\theta_{14})] - L_4.\omega_{14} = -L_2.\omega_{12}[cos(\theta_{12}-\theta_{14}) + i.sin(\theta_{12}-\theta_{14})] \)

Expressing only the imaginary terms gives the equation:

\(\large\ L_3.\omega_{13}.sin(\theta_{13}-\theta_{14}) = -L_2.\omega_{12}.sin(\theta_{12}-\theta_{14}) \)

Giving:

\(\large\ \omega_{13} = \omega_{12}. \cfrac {-L_2.sin(\theta_{12}-\theta_{14})}{L_3.sin(\theta_{13}-\theta_{14})}\)

which can be expressed as:   \(\large\ \omega_{13} = \omega_{12}. \cfrac {L_2.sin(\theta_{12}-\theta_{14})}{L_3.sin(\theta_{14}-\theta_{13})} ........ (2)\)

Correspondingly, to solve for θ₁₄ in terms of θ₁₂ multiply equation (1) above by e^-i.θ₁₃ to give the following expression for θ₁₄:

\(\large\ \omega_{14} = \omega_{12}. \cfrac {L_2.sin(\theta_{12}-\theta_{13})}{L_3.sin(\theta_{14}-\theta_{13})} ........ (3)\)

Equations (2) and (3) represent precisely the geometry of the velocity diagrams illustrated previously.

Acceleration diagram for four bar crank rocker mechanism

Our example of an acceleration diagram for the four bar crank rocker is based on a crank angle (θ₁₂) of 350°. The reason can be seen from Figures 8 and 9 showing angular velocities ω₁₃ and ω₁₄ are relatively small at a crank angle of 120°. Thus the radial components of acceleration are also relatively small, being proportional to ω². Consequently the acceleration diagram is not ideal for illustrating the method of construction.

Figure 10 below shows lines of action and directions, where known, for radial (subscript r) and tangential (subscript t) components of acceleration for bars L₂, L₃ and L₄ at a crank angle of 350°. Note that we designate point A as the ground reference point for links L₂ and L₄

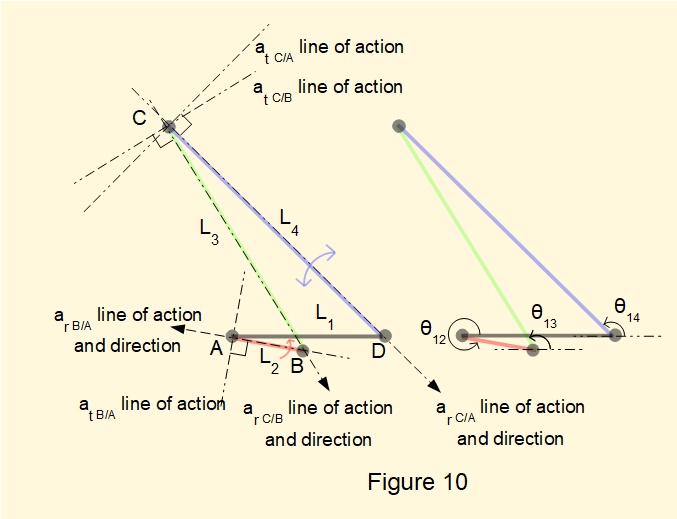
Angles θ₁₃ = 121.7° and θ₁₄ = 135.4° (obtained by position analysis from the previous tutorial)

From construction of the velocity diagram above we know:

• Link lengths   L₁ = 2 m,   L₂ = 1 m,   L₃ = 3.5 m,   L₄ = 4 m


• angular velocity ω₁₂ of crank L₂ = 2.π radians/s (constant).


• angular velocities ω₁₃ of link L₃ and ω₁₄ of link L₄ at crank angle 350° from calculation are:
       ω₁₃ = 4.26 radians/s    ω₁₄ = 4.92 radians/s

Thus radial components of acceleration a_{r B/A}, a_{r C/B}, a_{r C/A} are as follows:

a_{r B/A} = (ω₁₂)².L₂ = 39.4 m/s²

a_{r C/B} = (ω₁₃)².L₃ = 63.5 m/s²

a_{r C/A} = (ω₁₄)².L₄ = 96.8 m/s²

Because crank L₂ has constant angular velocity the tangential component of acceleration a_{t B/A} is zero.

Lines of action of tangential components of acceleration a_{t C/B} and a_{t C/A} are known. Their magnitudes will be determined from the diagram.

We start the acceleration diagram in Figure 11a by plotting to scale the radial components of acceleration along their lines of action with their known magnitude and direction. If necessary, refer to Figure 2 above which explains the direction and designation of points on the diagram. Points representing intermediate stages to point C are designated C^/ and C^//.

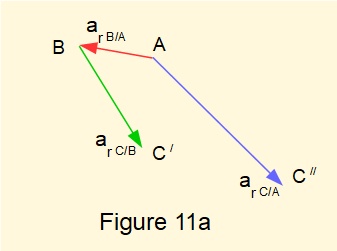
In Figure 11b we plot lines of action for tangential components a_{t C/B} and a_{t C/A}. The intersection of these lines represents point C. Thus magnitudes of a_{t C/B} and a_{t C/A} are determined by scaling lines C^/C and C^//C respectively.

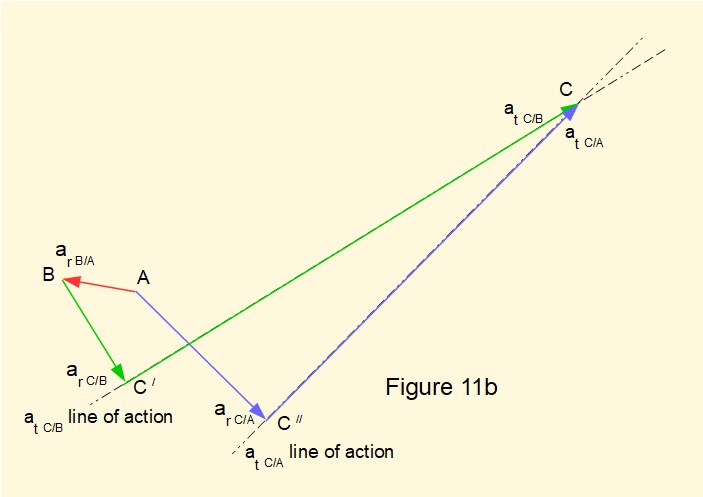
In Figure 11c we complete the diagram by plotting and scaling lines BC and AC which represent resultant accelerations a_C/B and a_C/A respectively. Note that a_{r B/A} = a_B/A as there is no tangential component of acceleration.

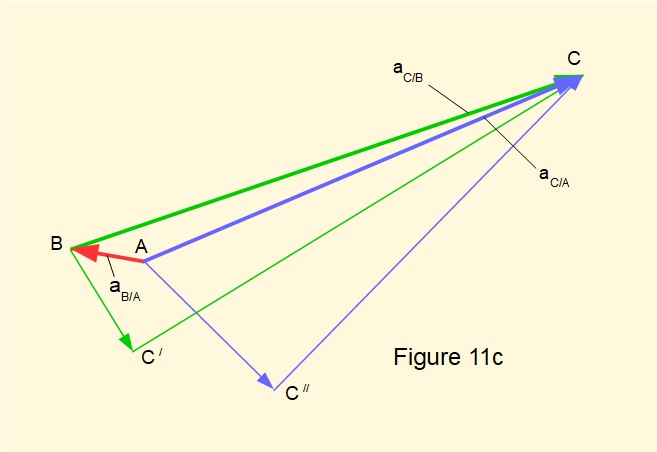
The acceleration diagram provides the means of determining angular accelerations α₁₃ for coupler L₃ and α₁₄ for rocker L₄ using expressions:

α₁₃ = L₃.a_{t C/B}

α₁₄ = L₄.a_{t C/A}

Scaling from the acceleration diagram gives a_{t C/B} = 282.0 m/s² and a_{t C/A} = 253.0 m/s².

Giving:   α₁₃ = 80.0 radians/s² and α₁₄ = 63 radians/s². These values can be verified to a reasonable degree by estimating rates of change of ω₁₃ and ω₁₄ from Figures 8 and 9 above.

The signs of α₁₃ and α₁₄ are deduced from the acceleration diagram using the vector* relationship:

*in this case treating the arrows in the diagram as vectors.

   α = r x a_t

where r represents position vectors BC^/ and AC^//. At this position of crank angle (350°), α₁₃ and α₁₄ are both positive (i.e. counter-clockwise rotation), again illustrated in Figures 8 and 9, whilst angular velocities ω₁₃ and ω₁₄ are negative (clockwise rotation). The characteristics of ω and α for the coupler and rocker are similar to those of the connecting rod in a slider and crank mechanism illustrated in a previous tutorial.

Slider and crank as a four bar mechanism

We can consider a slider and crank mechanism as a special case of a four bar crank rocker mechanism in the following way. Consider Figure 12a below.

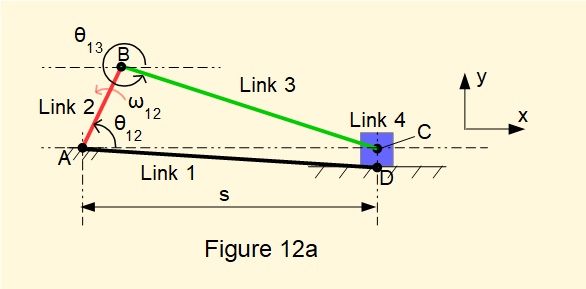
Link 2 (crank) and link 3 (coupling rod) are connected at both ends by revolute joints. Link 4 (slider) connects with the ground plane through a prismatic joint at a notional point D linked to ground point A forming link 1 of varying horizontal length s.

Now consider this arrangement of links using the vector loop method described in the previous tutorial.

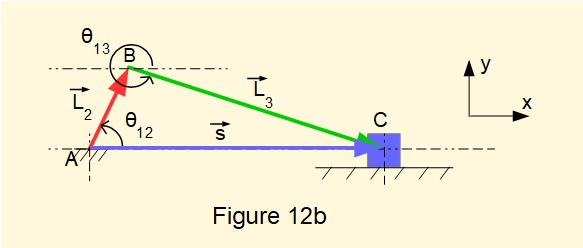
Figure 12b shows the vector loop with links 2 and 3 represented by position vectors L₂ and L₃, based on a notional break in the loop at joint C. We represent link 4 (the slider) as position vector s of variable magnitude in the horizontal direction from ground point A to point C, in effect "shorting out" ground link AD. This gives the following vector loop equation:

L₂ + L₃ = s

We can express this equation in terms of complex components where:

L₂ = L₂.cosθ₁₂.i + L₂.sinθ₁₂.j

L₃ = L₃.cosθ₁₃.i - L₃.sinθ₁₃.j (noting that L₃.sinθ₁₃ has direction - j)

s = s.i + 0.j

Separating i and j components gives two scalar equations with two unknowns:   θ₁₃ and s.

L₂.cosθ₁₂ + L₃.cosθ₁₃ = s ......... (1)

L₂.sinθ₁₂ - L₃.sinθ₁₃ = 0 .......... (2)

Equation (2) gives:   sinθ₁₃ = [L₂/L₃].sinθ₁₂ ......... (3)

Thus we can determine angle θ₁₃ for any given crank angle θ₁₂ where L₂ and L₃ are defined. The magnitude of s can then be determined by substituting this value of θ₁₃ into equation (1).

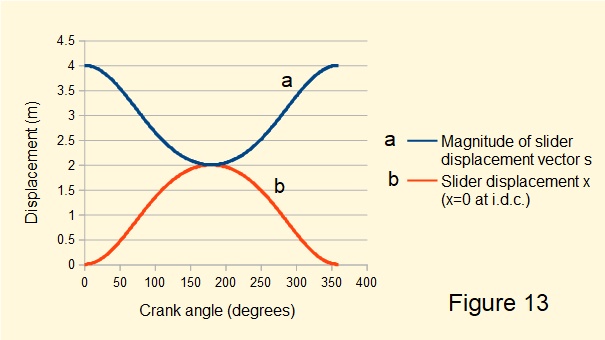
In Figure 13 below plot(a) is the magnitude of vector s, that is displacement of the slider on the horizontal axis measured from the centre of rotation of the crank, computed from the above equations for one complete crank cycle.

Plot (b) shows the same computation with the datum on the horizontal axis adjusted to the inner dead centre (i.d.c.) position of the slider. This plot is identical to that in a previous tutorial where we derived the following expression for slider displacement x:

\(\large\ x = L_2[1-cos\theta_{12} + n - \sqrt{(n)^2 - sin^2\theta_{12}}] \)

where  \(\large\ n = \cfrac{L_3}{L_2} \)

Next:  Return to: Content - mechanics of machines

I welcome feedback at:

alistair@alistairstutorials.co.uk